汽配行业资讯更多

全国推介·上海站 | “温州紧博会”赴上海紧固件专业展宣传推广，打响温州品牌！

2024-03-22 16:24

借势发力，一路“狂飙” | 第19届温州机械装备展宣传邀约宁波、台州行！

2024-03-22 16:24

直播预告 | 未来园林公益植树暨CAPAS 2024展前发布会

2024-03-19 18:05

助力掘金越南市场——温州市人民政府自办 “中国（温州）国际电子智能制造展—越南站”11月开幕

2024-03-15 14:27

温州国际会展中心2024重点境外展会项目公布,开启海外市场布局新篇章！

2024-02-23 16:45

行业信息 | 温州这个产业增加值“领涨”，居五大传统产业榜首

2024-02-23 16:45

Automechanika 海外展团队恭祝大家：龙年大吉，喜乐安康！

2024-02-09 20:21

展会现场|印度（新德里）国际汽车零部件、汽车技术及服务展览会

2024-02-08 14:31

成绩斐然，喜讯频传 | 温州市会展行业协会六届一次会员大会圆满成功，温州会展中心展览分公司喜获多项荣誉！

2024-02-01 09:09

Automechanika Dubai 2023 勇创新纪录的行业盛会！

2024-01-26 15:48

粒子群优化线控转向变角传动比模糊控制器设计

来源：世展网分类：汽配行业资讯 2023-09-06 11:02 阅读：7682

2025年中国上海国际健康产业博览会-世博威健博会CIHIE

2025-06-24-06-26

距离45天

摘要：为了提高汽车低速时的转向轻便性与高速时的转向稳定性，设计了一种线控转向变角传动比粒子群模糊控制器。采用线控转向系统可变传动比的特性，利用模糊控制将方向盘转角和车速进行模糊处理，输出精确的传动比，同时根据粒子群算法思想，提出一种粒子群算法优化模糊控制算法。设计仿真控制器，将模糊控制与粒子群算法相结合，通过低速和高速的双移线仿真工况，以及角阶跃仿真工况进行联合仿真控制系统研究。结果表明：粒子群优化模糊控制所设计的变角传动比相比于定传动比和未优化的模糊控制器，能够更好地实现汽车低速转向灵敏和高速转向的稳定性，减轻了驾驶员的疲劳程度，提高了汽车的操纵稳定性和行驶安全性。

1 线控转向汽车建模

考虑到汽车的复杂性和非线性不便于对线控转向系统变角传动比进行研究，所以将其进行一定程度上的简化和线性化处理，通过车辆动力学模型公式搭建线控转向系统与整车模型，为后续线控变角传动比的研究提供模型基础。

1.1 转向执行机构模型

线控转向系统主要包括方向盘总成模型、ECU、转向执行机构模型，其中转向执行机构是实现汽车转向的重要组成部分，其线控转向系统工作原理见图1。图1 线控转向系统工作原理示意图转向执行机构总成主要包括转向电机、减速器、齿轮齿条转向器、转向轮组件。转向执行电机的动力学方程为：

式中：Tm为电机的输出转矩；Jm为电机的转动惯量；Bm为电机转动的阻尼系数；Kxr为齿条的等效刚度； θm为电机的转角；Gm为减速器的减速比；xr为齿条的位移量；rp为小齿轮分度圆半径; fm为摩擦阻力。转向机构的执行电机选用直流无刷电机作为驱动源，其电动势平衡方程为：

式中：um为电机的电压；im为电机的电流；Rm为电机的电阻；Lm为电机的电感；Km为电机反电动势的比例系数。转向电机输出转矩与电流的关系为：Tm=Ktim式中：Kt为电机的电磁转矩系数。齿轮齿条转向器的动力学模型为：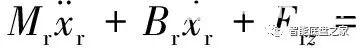

式中：Mr为齿条的质量；Br为齿条的阻尼系数；fr为转向器的等效摩擦力；Frz为主销回正力，是由左右转向车轮的主销回正力矩所产生的，即：

式中：Tfl、 Tfr分别为左、右前轮绕主销的回正力矩；lfl、lfr分别为左右前轮转向摇臂长度。左右转向轮动力学方程模型为：

式中：Jrw为前轮绕主销的转动惯量；Brw为前轮绕主销的阻尼系数；Krw为主销扭转刚度系数；δf为前轮转角；Grw为齿条到左右前轮的传动比。转向执行机构参数如表1所示。表1 转向执行机构参数由于PID控制器具有很好的适应性和较强的鲁棒性，所以转向执行电机采用PID控制其电压进行工作，线控转向传动比取其定值i=15，通过Ziegler-Nichols方法确定了PID控制器参数的值，取Kp=238.20、Ki=296.18、Kd=47.89。

1.2 整车动力学模型

参考某款B级车型对Carsim整车参数进行修改，搭建整车模型，为后续线控变角传动比的研究提供整车模型基础。车辆主要参数见表2。表2 车辆主要参数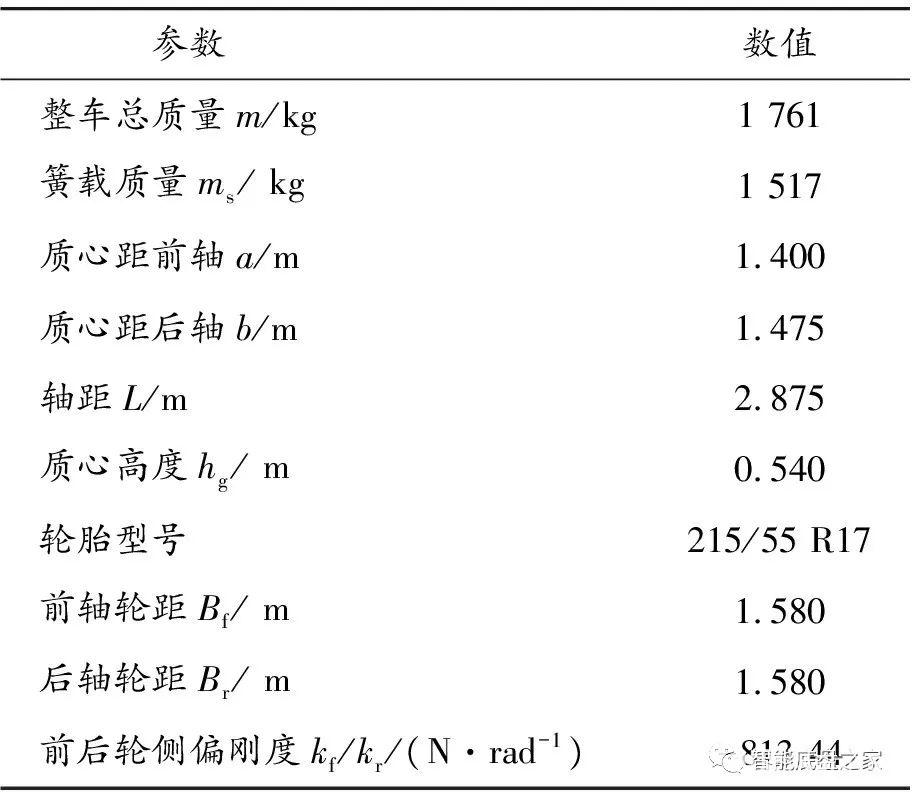

1.3 轮胎模型

轮胎模型能够反映出汽车车轮在路面上的附着系数变化情况，并且轮胎的参数与受力均影响着汽车驾驶性能，因此选用“魔术公式”轮胎模型，其动力学方程为：y=Dsin{C·arctan[Bx-E(Bx-arctanBx)]}根据“魔术公式”与车辆单轮垂直载荷可以求出轮胎的侧偏刚度，见表2。

1.4 理想传动比

假设汽车只有2个自由度，即沿y轴的侧向运动和绕z轴的横摆运动，则汽车的2自由度简化模型如图2所示。根据图2及汽车运动学知识可得出2自由度汽车运动微分方程：

式中： β为质心侧偏角；u为纵向车速；ωr为横摆角速度；δf为前轮转角，kf、kr分别为前后轴侧偏刚度。图2 2自由度模型示意图稳态时横摆角速度为定值，令

则：

又汽车转向传动比是方向盘转角与前轮转角的比值，即：

将式(8)代入式(9)，可以得出线控转向理想传动比：

德国汽车研究所由实验得到稳态横摆角速度增益Kr为0.16～0.33 s-1，所以本文取Kr=0.32。

2 粒子群优化模糊控制器设计

模糊控制器根据专家经验设定，具有一定的局限性，模糊规则也不是最优的，无法使系统横摆角速度和质心侧偏角达到最优值。针对以上问题，以积分性能指标为目标函数，设计了粒子群算法优化模糊控制器以改善汽车转向特性和操纵稳定性。

2.1 粒子群算法

粒子群算法PSO是一种群体智能的优化算法，它相对简单、容易实现且搜索效率较高，具有局部和全局搜索的能力。在一个d维的搜索空间内，种群x=(x1,x2,…,xn)是由n个粒子所组成，其中第i个粒子为d维的一个向量x=(xi1,xi2,…,xid)T，即该粒子在d维空间内的位置，也是一个潜在解。根据所选择的目标函数便可以计算出每个粒子当前位置的适应度值，第i个粒子的速度为vi=(vi1,vi2,…,vid)T，对应的个体极值为pi=(pi1, pi2,…, pid)T，种群极值为 pg=(pg1, pg2,…,pgd)T。粒子群的进化过程为：vij(k+1)=w·vij(k)+c1r1(k)[pij(k)-xij(k)]+c2r2(k)[pgi(k)-xij(k)]xij(k+1)=xij(k)+vij(k+1)式中：vij为粒子速度；w为惯性权重；c1、c2为学习因子；rr、r2为[0,1]内的随机数；pij为个体最优解；pgi为群体最优解；xij为粒子位置；k为当前迭代次数。粒子群算法首先随机生成一群粒子，并计算粒子适应度值，寻找出个体最优值和群体最优值，然后通过迭代不断更新自身速度和位置，并对粒子进行边界处理，防止粒子飞出边界，最后寻找出全局最佳位置，即全局最优值。通过不断地迭代求值，得到最终的目标值，粒子群算法的运算流程见图3。图3 粒子群算法的运算流程框图标准粒子群算法操纵简单，但容易陷入局部最优，所以引入了可变权重与可变学习因子，惯性权重和学习因子c1线性递减、学习因子c2线性增加，以保证粒子的全局寻优能力。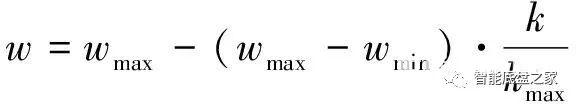

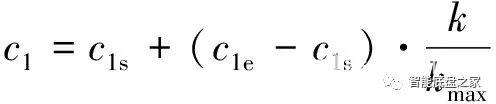
式中：wmax为惯性权重初始值，取0.9；wmin为惯性权重结束值，取0.4；c1s、c2s为学习因子初始值，分别取2.5、0.5；c1e、c2e为学习因子结束值，分别取0.5、2.5；kmax为最大迭代次数。

2.2 模糊变角传动比设计

模糊控制器由模糊化、模糊推理、模糊判决、去模糊化4部分组成，其工作原理见图4。它将输入量的精确量转换为模糊量，将模糊规则置于规则库中，通过隶属度函数得到控制参数的模糊量，最后将其转化成实际控制的精确量并作用于被控系统使其工作。图4 模糊控制工作原理示意图模糊控制的输入输出均采用7个模糊子集进行控制，分别用NB、NM、NS、ZO、PS、PM、PB来表示负大、负中、负小、零、正小、正中、正大，隶属度函数采用灵敏度较高的等腰三角形并将输入输出论域进行均分设置。为了避免汽车在低速转向时过于迟钝、高速转向时过于灵敏，根据式(10)将车速小于20 km/h的传动比设置为imin=6，将车速大于100 km/h的传动比设置为imax=26，所以将其车速论域设为[5.56,27.78]，单位m/s，传动比论域设为[6,26]，方向盘可以左右转向，最大限位540°，论域设为[-9.42,9.42]，单位rad。将车速和方向盘转角作为模糊控制器的输入量，传动比作为其输出量，搭建模糊控制器，模糊规则见表3。表3 模糊规则优化前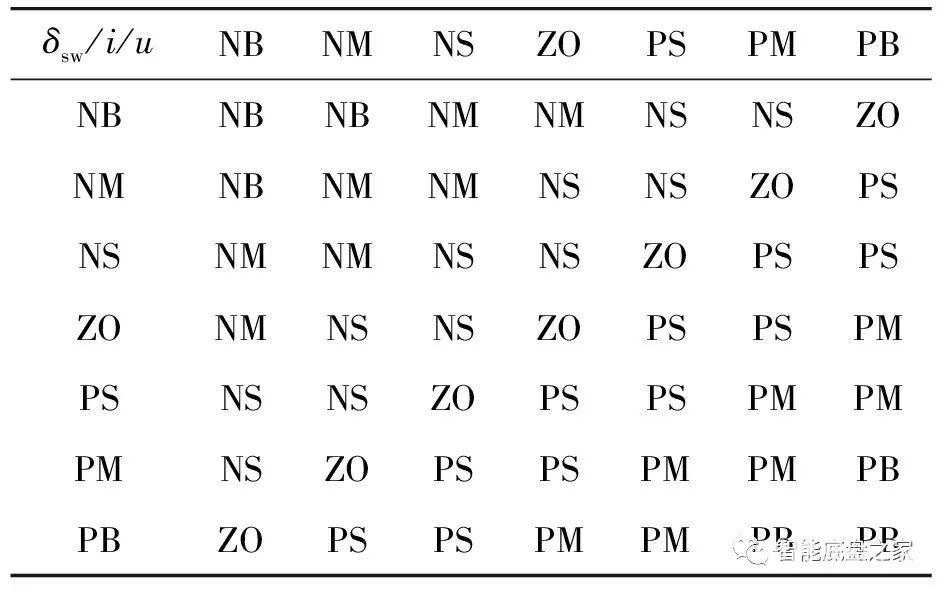

2.3 确定适应度函数

积分性能指标ITAE为时间和误差绝对值的乘积再积分，它能够缩短系统的反应时间，减小超调量，使系统趋于稳态。将ITAE作为目标函数，采用粒子群算法优化模糊控制器，从而得到最优的控制效果。其积分性能指标为：J=

t|e(t)|dt2.4 优化模糊控制器由于模糊控制器隶属度函数与模糊规则受人为设置影响较大、需要反复调试且复杂，所以将粒子群算法与模糊控制相结合使用，可以对隶属度函数与模糊控制规则进行全局寻优，从而摆脱模糊规则受到人为经验的限制。PSO-fuzzy控制结构见图5。图5 PSO-fuzzy控制结构示意图粒子个体编码采用整数编码的方式，由于模糊控制隶属函数曲线关于论域中心轴线对称，所以只对位于中心轴线的右半边曲线进行编码，方向盘隶属度函数顶点依次编码为x1、x2、x3，底边依次编码为x4、x5、x6、x7、x8、x9，见图6。将方向盘转角、车速、传动比的隶属度函数依次编码组成一维数组，共27个未知数。然后将模糊规则的子集按顺序进行编号，即NB、NM、NS、ZO、PS、PM、PB分别编为1、2、3、4、5、6、7。模糊规则表中传动比的子集也全部转换为数字形式，并按行首尾相接依次排列为一维数组，再与隶属度函数数组拼接，组成一个新的一维数组，即为一个粒子。图6 隶属函数编码曲线编码结束后设置粒子群算法参数，设定粒子群体规模为50，维数为76，最大迭代次数为50，粒子速度为v∈[-1,1]，模糊规则的粒子位置x∈[1,7]。选择变车速变转向仿真工况进行隶属度函数与模糊规则全局寻优，路面附着系数为0.75。最终得到全局最优的隶属度函数和模糊规则，见图7—图9、表4。图7 方向盘转角隶属度函数曲线图8 车速隶属度函数曲线图9 传动比隶属度函数曲线表4 模糊规则优化后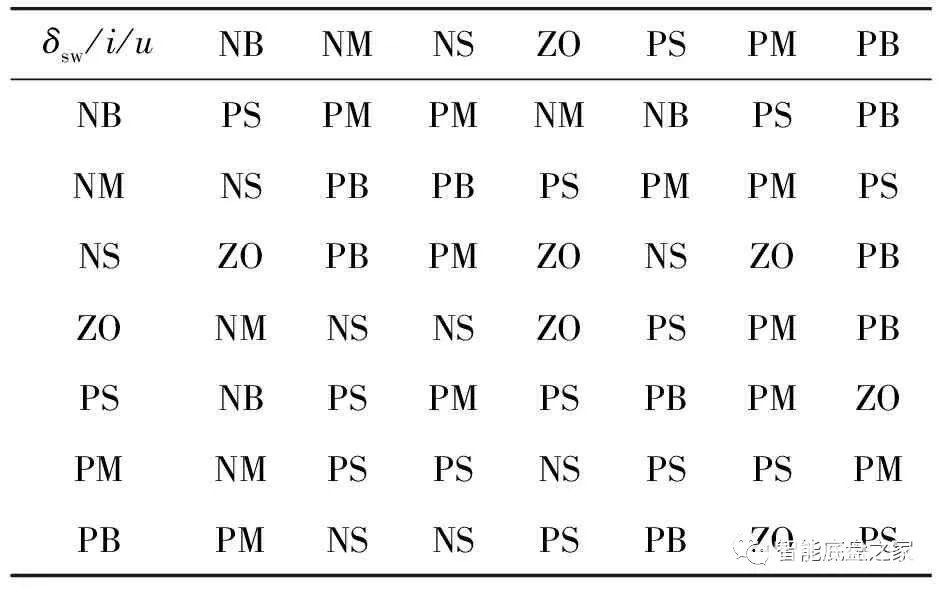

2.5 系统模型设计

根据优化后的隶属度函数与模糊规则建立模糊控制器，结合系统的控制策略搭建模型进行仿真分析，线控转向系统变角传动比控制策略见图10。

图10 SBW系统变角传动比控制策略框图

3 仿真分析

为了验证所设计的粒子群模糊控制器的性能，通过联合仿真，采用双移线和角阶跃仿真工况进行仿真分析。同时，与定传动比、未优化的模糊控制器的仿真结果进行对比分析。

3.1 双移线

汽车在高速行驶时为了保持车身稳定，方向盘角度不会过大，低速行驶时方向盘转角较大，便于更好转向。所以，分别选取低速30 km/h和高速80 km/h进行双移线工况仿真，试验结果见图11—图16。

图11 30 km/h时的方向盘转角曲线图12 30 km/h时的横摆角速度曲线图13 30 km/h时的质心侧偏角曲线由图11—图13可知，在汽车低速行驶时，采用PSO-fuzzy设计的变传动比的方向盘转角明显小于定传动比和未优化fuzzy控制的方向盘转角。其次，横摆角速度和质心侧偏角的峰值略小于其余两者，说明所设计的变角传动比汽车满足低速行驶时转向的轻便性。图14 80 km/h时的方向盘转角曲线图15 80 km/h时的横摆角速度曲线图16 80 km/h时的质心侧偏角曲线由图14—图16可知，在汽车高速行驶时，PSO-fuzzy设计的变传动比的方向盘转角又大于定传动比与未优化fuzzy控制的方向盘转角，且横摆角速度和质心侧偏角最值也略小，PSO-fuzzy的控制效果较好，且优于其他两者，使车辆能够在高速转向行驶时保持较好的稳定性。为了更直观地观察横摆角速度和质心侧偏角的变化，在Matlab中使用rms命令对其计算二次均方根值，如表5所示。可见，在30 km/h的双移线工况下，横摆角速度在PSO-fuzzy控制、fuzzy控制下分别下降了3.83%和2.69%，且质心侧偏角分别下降了3.83%和2.70%，说明PSO-fuzzy的控制效果更好。在80 km/h的双移线工况下，横摆角速度在PSO-fuzzy控制、fuzzy控制下分别上升了0.70%和0.42%，而质心侧偏角分别下降了2.75%和1.85%，综上可知，优化之后的变角传动比满足低速的转向轻便性和高速的稳定性。表5 二次均方根值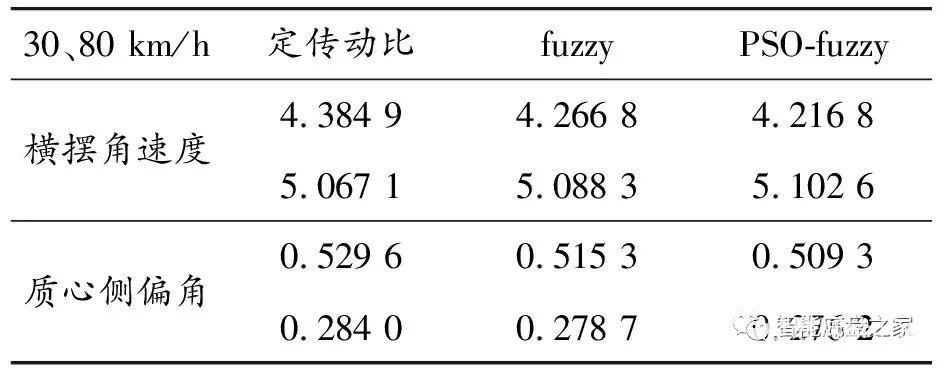

3.2 角阶跃

采用车速80 km/h进行角阶跃仿真，方向盘转角为30°，其试验结果见图17、18。图17 80 km/h时的横摆角速度曲线图18 80 km/h时的质心侧偏角曲线由图17和图18可知，三者的响应速度大致相同，横摆角速度在PSO-fuzzy和未优化的fuzzy控制下分别下降了30.80%和24.63%，PSO-fuzzy控制器的横摆角速度的超调量更小，横摆角速度也远远小于定传动比和未优化fuzzy控制的横摆角速度。质心侧偏角在PSO-fuzzy和未优化的fuzzy控制下分别下降了42.71%和35.87%，PSO-fuzzy控制器的质心侧偏角的超调量也小于其他两者，质心侧偏角也更小，可见PSO-fuzzy控制的效果更好。但是三者的质心侧偏角在方向盘突然转向时出现了一个反向的脉冲，通过对数据及其软件分析得知：由于在进行角阶跃仿真时，仿真软件模型为开环系统，没有了驾驶员模型的自动校正，所以出现了微小脉冲。

4 结论

1) 通过双移线和角阶跃工况验证了PSO-fuzzy控制器所设计的变角传动比，可以更好地改善驾驶员的转向特性。

2) 线控转向变角传动比在低速时可以采用更小的方向盘转角实现转向，改善汽车的机动性，在高速时又可以防止转向盘过于灵敏，从而提高了汽车的操纵稳定性和行驶安全性。3) 采用粒子群模糊控制器设计的变角传动比控制效果优于未优化的fuzzy的控制器，也避免了模糊控制器设计者经验误差的限制。来源：智能底盘之家

主办单位：AEE汽车技术平台米创博隆展览（上海）有限公司展会官网： 联络我们：米创博隆展览（上海）有限公司Micreative-Bolong Exhibition (Shanghai ) Co.,LtdAMEE2023展位预订咨询：底盘设计与智能底盘展区alin Xie ：新能源汽车底盘技术展区Kevin Li： Anna Lv：底盘轻量化技术展区Cindy Gu： Lina Wang：底盘部件先进工艺展区Jeff Shen：汽车底盘零部件展区LUCY Liu ：商用车底盘技术展区 Allen：AMEE2023展位及同期会议预订点击 “阅读全文”

阅读原文

会务组联系方式

电话：13248139830(展商名录/门票）